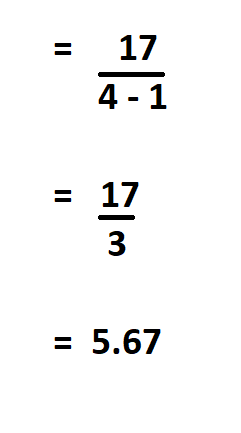What is Sample Variance?
Ahead of discussing how to calculate sample variance (s²), let’s define what variance is. Variance is a measure of how far each value in the data set is from the mean.
Sample variance is a measure of how far each value in the data set is from the sample mean. If the numbers in a list are all close to the expected values, the variance will be small. If they are far away, the variance will be large.
With samples, we use n – 1 in the formula because using n would give us a biased estimate that consistently underestimates variability. The sample variance tend to be lower than the real variance of the population.
Reducing the sample n to n – 1 makes the variance artificially large, giving you an unbiased estimate of variability. It is better to overestimate rather than underestimate variability in samples.
There are two types of sample variance and they are:
- Unadjusted sample variance also known as biased sample variance. It measures the average dispersion of a sample of observations around their mean. It is computed by averaging the squared deviations from the mean.
- Adjusted sample variance or the unbiased sample variance. The adjusted sample variance is a measure of the dispersion of a sample around its mean. It is obtained by summing the squared deviations from the mean, dividing the result thus obtained by the number of observations minus one.
Formula to Calculate S².
To calculate sample variance;
- Calculate the mean( x̅ ) of the sample
- Subtract the mean from each of the numbers (x), square the difference and find their sum.
- Divide the result by total number of observations (n) minus 1.
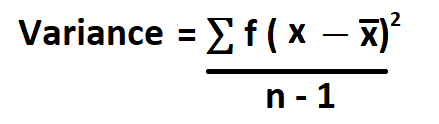
Example:
Determine the variance of the following sample data.
2, 5, 6, 1
We begin by finding the mean of the sample data.
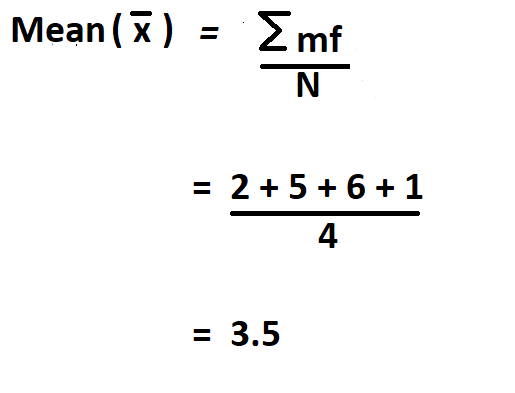
Then subtract the mean from each of the numbers, square the difference and find their sum.
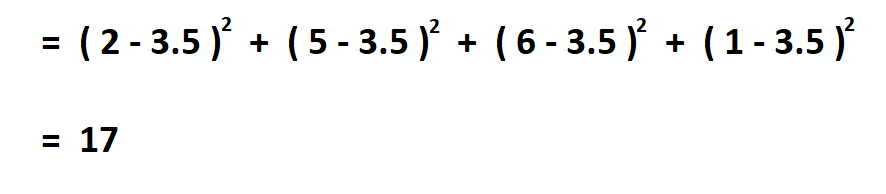
Divide the result by the total number of observations minus one.