Eigen vector is a nonzero vector that is mapped by a given linear transformation of a vector space onto a vector that is the product of a scalar multiplied by the original vector.
Eigenvectors make understanding linear transformations easy.
Formula to calculate eigenvectors.
- You should first make sure that you have your eigen values.
- Then subtract your eigen value from the leading diagonal of the matrix.
- Multiply the answer by the a 1 x 2 matrix of x1 and x2 and equate all of it to the 1 x 2 matrix of 0.
Example:
Calculate the eigen vector of the following matrix if its eigenvalues are 5 and -1.
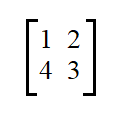
Lets begin by subtracting the first eigenvalue 5 from the leading diagonal.
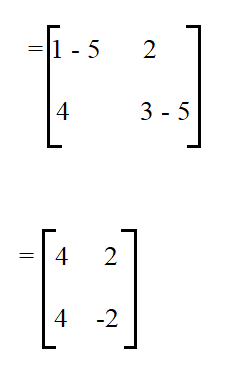
Then multiply the resultant matrix by the 1 x 2 matrix of x, equate it to zero and solve it.

Then find the eigen vector of the eigen value -1.
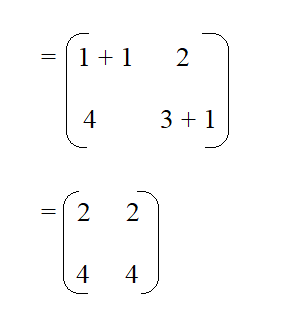
Then equate it to a 1 x 2 matrix and equate it to 0.


