Eigenvalues are a special set of scalars associated with a linear system of equations also known as characteristic roots, characteristic values, proper values, or latent roots.
Eigenvalues have their importance in linear differential equations where you want to find a rate of change or when you want to maintain relationships between two variables.
Formula to calculate eigen values.
- You begin by multiplying lambda by the identity matrix of the n x n matrix, it can be a 2 x 2 or a 3 x 3 matrix.
- Then subtract the result in 1 above from your matrix.
- Find the determinant of your result in 2.
- Solve for lambda from the equation you get in 3 to get your eigen values.
Example:
Calculate the eigen values of the 2 x 2 matrix below.
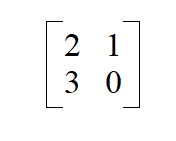
We begin by calculating the identity matrix of a 2 x 2 matrix by lambda.
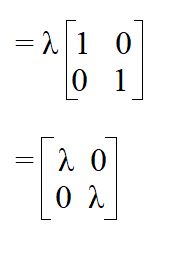
We then subtract our result from our matrix.

We find the determinant of our result above and solve the equation.
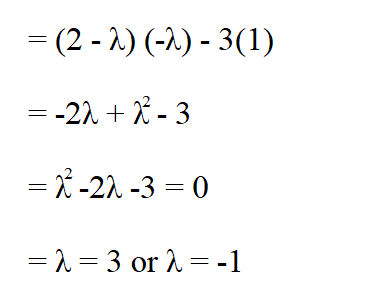
Therefore, the eigen values are 3 and -1.