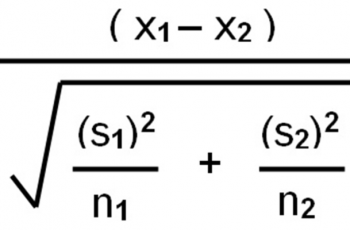In statistics, the p-value is the probability of obtaining results at least as extreme as the observed results of a statistical hypothesis test, assuming that the null hypothesis is correct.
The value of the z-score tells you how many standard deviations you are away from the mean.
Formula to calculate p-value from z-score.
- For a left-sided tail test, we use P-value = ϕ(z-score)
- For a right-sided tail test, we use P-value = 1 – ϕ(z-score)
- For a two tailed test, we use P-value = 2 – 2 x ϕ (|z-score|)
ϕ is the cumulative distribution function (cdf) of the standard normal distribution.
Example:
Calculate the p-value of a right-sided tail test if the ϕ is 0.2 and the z-score is 2.
P-value = 1 – ϕ (z-score)
= 1 – 0.2( 2)
= 0.6
Therefore, the p-value is 0.6.