We can define confidence interval as a measure of the degree of uncertainty or certainty in a sampling method.
To calculate confidence interval, we use sample data that is, the sample mean and the sample size.
For a sample size that is more 30 ( a large sample size ), we use the values of z* for the given confidence levels. Which we can get from statistical tables. Example:
| Confidence Level | Z* Value |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Formula to calculate confidence interval.
Confidence interval is sample mean, plus or minus the margin of error ( z* value multiplied by standard deviation divide by the square root of the sample size.)
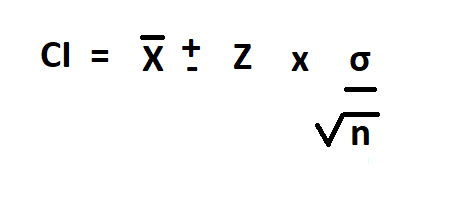
Example:
Suppose we take a random sample size of 100 fingerlings, we are asked to determine that the mean length of the fingerlings is 5 cm, with 95% confidence level and a standard deviation of 3.
In this case, the confidence level is 95% so the corresponding Z* value is 1.96.
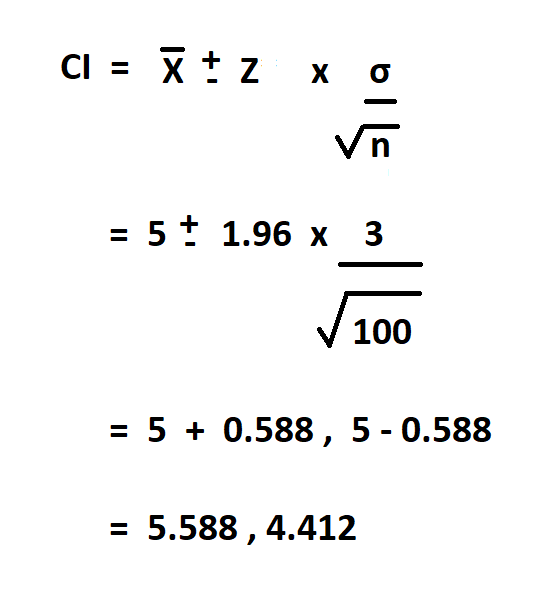
Therefore, with 95% confidence interval, the average length of the fingerlings is between 5.588 cm and 4.412 cm.