We can either define median as the middlemost number in the set or the number that is halfway into the set.
A set of data can either be grouped or ungrouped.
Formula to calculate median of ungrouped data.
We start by either arranging the ungrouped data in ascending or descending order, whichever you prefer, then count the number of observations (n), add 1 and then divide the result by 2.
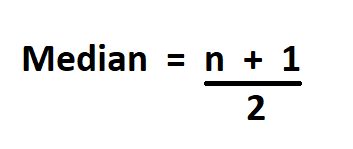
Example:
Find the median in the following set of data.
2, 4, 5, 6, 8, 9, 2, 1
We’ll start by arranging the data in ascending order.
1, 2, 2, 4, 5, 6, 8, 9
Then add 1 to the number of observations, which in this case are 8.
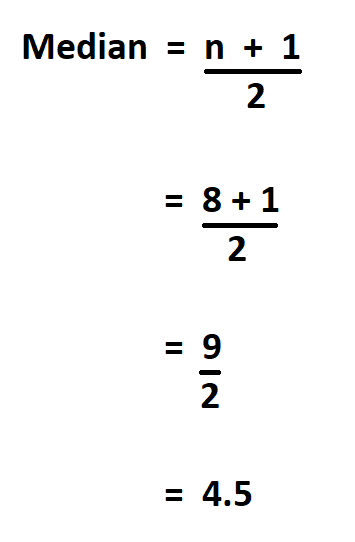
Therefore, the median of the data set is 4.5 .
Formula to calculate median of grouped data.
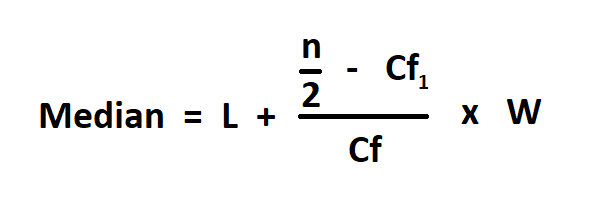
- L is the lower class boundary of the group containing the median
- n is the cumulative frequency in the last class.
- Cf1 is the cumulative frequency of the class before the median class.
- Cf is the frequency of the median class.
- W is the group width.
Example:
Find the median of the frequency distribution table below.
| Class | Class Limit | Frequency | C. Frequency |
| 1 – 5 | 0.5 – 5.5 | 2 | 2 |
| 6 – 10 | 5.5 – 10.5 | 4 | 6 |
| 11 – 15 | 10.5 – 15.5 | 8 | 14 |
| 16 – 20 | 15.5 – 20.5 | 8 | 22 |
To find the median class, we take the cumulative frequency of the last class, add 1 and divide by 2, then observe the cumulative frequency column to know in which class does it lie.
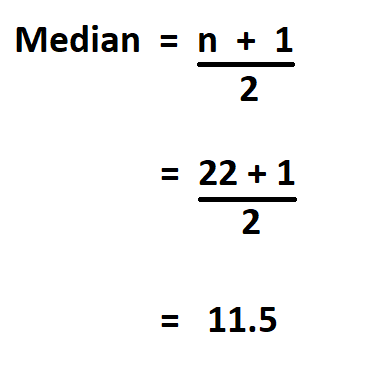
Hence, the median class is 11 – 15 and its lower class boundary is 10.5.
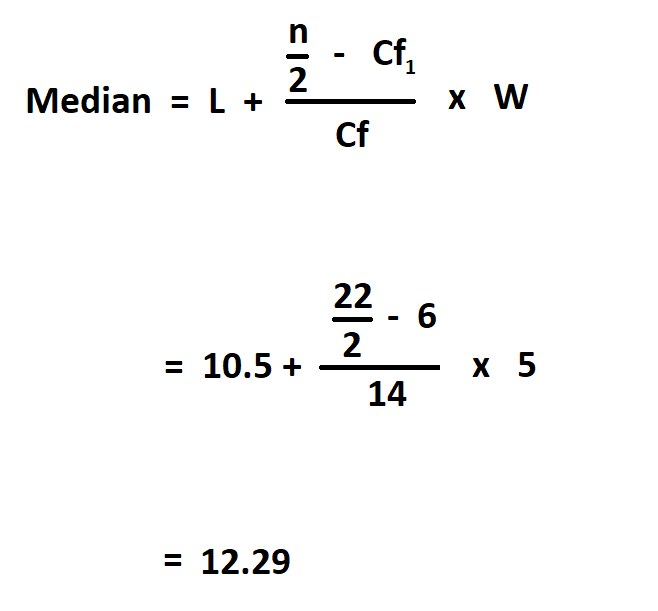
Therefore, the median for the grouped data is 12.29 .
