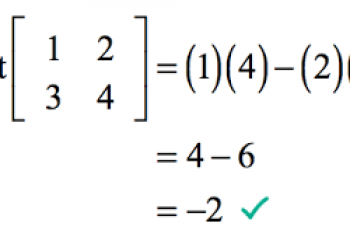What is a Matrix?
In this article we will define and discuss how to calculate the inverse of a 2 x 2 matrix. The inverse of a matrix A is a matrix that, when multiplied by A results in the identity.
An identity matrix is a matrix equivalent to 1. There is no concept of dividing by a matrix but, we can multiply by an inverse, which achieves the same thing.
Formula to Calculate Inverse Matrix of a 2 x 2 Matrix.
We begin by finding the determinant of the matrix. A determinant is a scalar value that can be computed from the elements of a square matrix. It helps in finding the inverse of a matrix that has the same number of rows and columns.
Swap the positions of the elements in the leading diagonal.
And put a negative sign in front of the elements in the other diagonal.
Lastly, multiply the resultant matrix by 1 divided by the determinant.
Example:
Find the inverse of the following matrix.
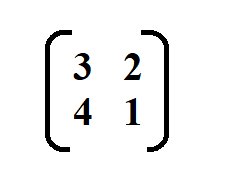
We begin by finding the determinant of the matrix.
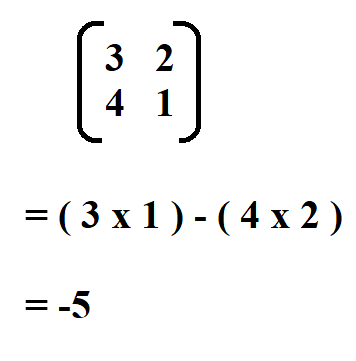
Therefore, the determinant of the matrix is -5.
Then we swap the positions of the elements in the leading diagonal and put a negative sign in front of the elements on the other diagonal.
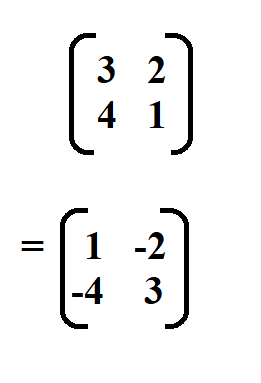
And lastly, multiply the resultant matrix by 1 divided by the determinant.
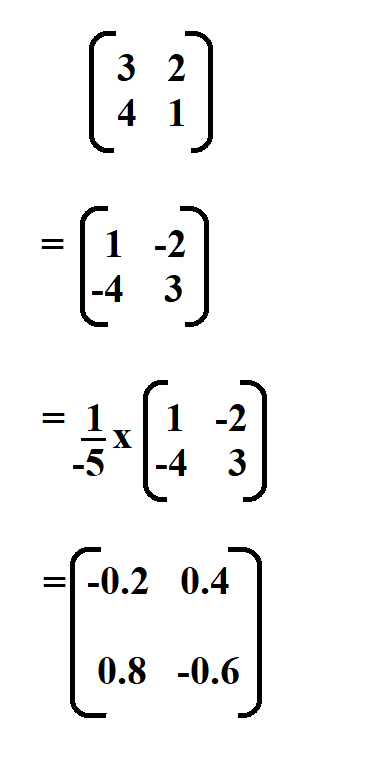
You may also encounter a problem where some of the elements in the matrix are variables. Treat this just like a normal determinant problem. Plug those variables in the designated spots in the formula then simplify as usual.