A determinant is a scalar value that can be computed from the elements of a square matrix.
The determinant helps in finding the inverse of a matrix that has the same number of rows and columns.
Formula to calculate Determinant.
To calculate determinant, we multiply the elements on the first diagonal and subtract the product of the elements on the other diagonal.
- How To Calculate Determinant Of a 2 x 2 Matrix.
Consider the matrix below.
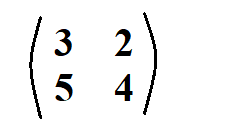
We start by identifying the first diagonal (runs from left to right).
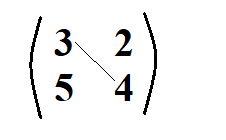
We find the product;
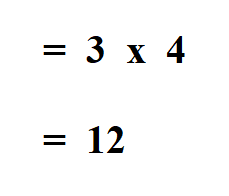
We then identify the other diagonal.
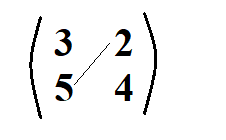
We then find the product of the elements.
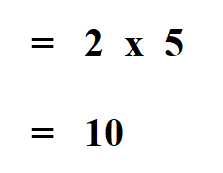
Then we find the difference of the products.
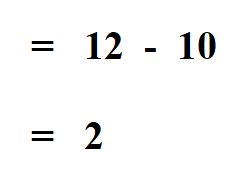
Therefore the determinant of the matrix is 2.
How To Calculate Determinant Of a 3 x 3 Matrix.
Consider the matrix below.
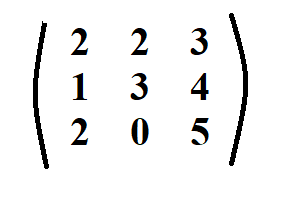
The elements in the first row, act as scalar multipliers.
We take the first element which is 2 and find the determinant of the 2 x 2 matrix that is not on the row and column of 2 and then multiply it by 2.
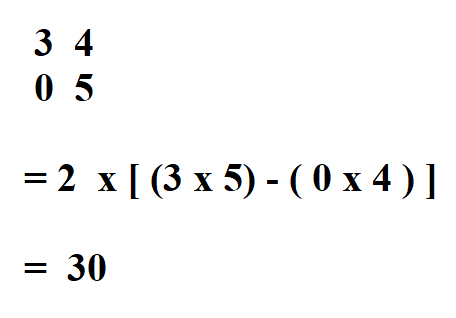
The second element is also 2, so we take 2 x 2 matrix that is not in its row or column.
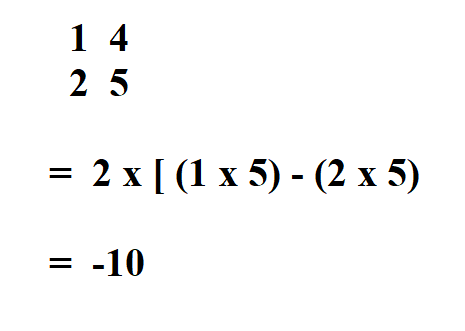
The third element is 3, so we take 2 x 2 matrix that is not in its row or column.
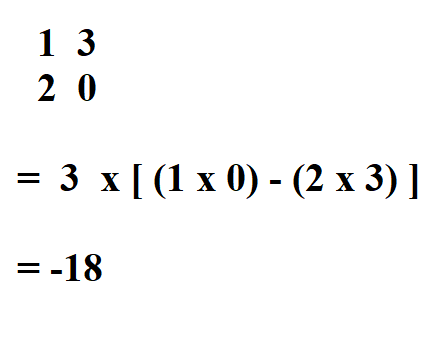
Then we put them together them. By adding the first result to the third result and subtract the second result. But since the second result is negative, we know that two negatives make a positive, so we will add the second result.
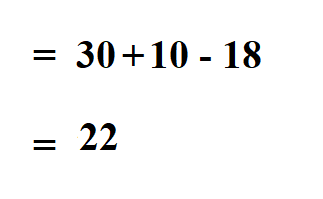
Therefore the determinant of the matrix is 22.
