We all know that speed is calculated by dividing the distance traveled by the time taken to cover that distance.
But this is only accurate in a ideal situation where the object traveled at a constant speed from start to finish. That’s hardly practical in real life.
In an example of a car moving from point A to point B, there are speed bumps, straight roads, junctions and all sorts of things to make you slow down and speed through out the journey; The speed is hardly constant.
For that reason, we use ‘Average Speed’ to determine speed in which the vehicle (or any other object) was moving. Although we still use the same formula to calculate the average speed.
Formula to Calculate the Average Speed.
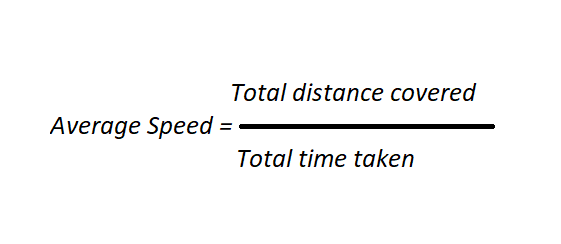
Normally this would pass as the average speed. Because the distance and time taken is all the information we have.
If we had more information about the way the car was moving, then we might come up with a different figure, a more scientific one. Calculating average speed depends on the information we have. I’ll demonstrate this with two examples of the same scenario.
Scenario:
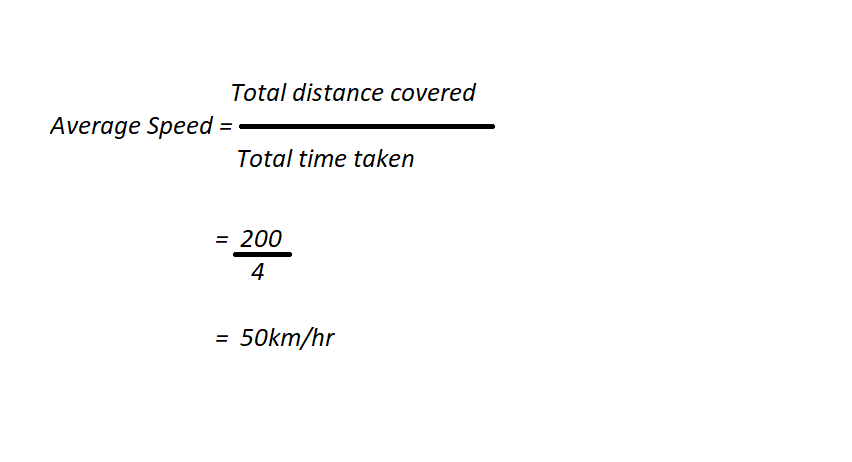
Chris started driving from Nairobi at 7.00 a.m. and arrived in Namanga, 200km away at 11:00 a.m.
Example 1:
What was Chris’ Average Speed?
We all know that Chris did not drive at a constant speed throughout the journey; Infact he probably had a bathroom break on the way. But we know the 200km journey took him 4 hours and that’s all the info we have.
So,
Example 2
Chris covered 50km in one hour, took a one hour lunch break then covered the rest of the journey in 2 hours. What was his Average Speed?
Since we have more information about this journey, we can calculate the average speed more accurately. Lets’ first calculate the speed in each of the three segments of his journey.
In the first hour, his speed was 50km/h. During the bathroom break, he was not moving so there’s no speed to calculate. He then covered 150 km in 2 hours which makes his speed 75km/h
His average speed is therefore calculated as we we would normally calculate average. But since he was not actually moving during the lunch break, we leave that part out.

The same journey has produced two different average speeds depending on the amount of information we have. That’s why it’s an average; a rough estimate.
To get the most accurate mathematically proven average speed, you’d have to calculate the speed at each second of the journey and get the average of all those speeds per second. But that’s usually unnecessary in practical life.