What is an Interquartile Range?
Before discussing how to calculate interquartile range, let’s define it. The interquartile range (IQR) is a measure of variability, based on dividing a data set into quartiles. Where a range is a measure of where the beginning and end are in a set, an interquartile range is a measure of where the bulk of the values lie.
Quartiles divide a rank-ordered data set into four equal parts. The values that divide each part are called the first, second, and third quartiles; and they are denoted by Q1, Q2, and Q3, respectively.
Due to its resistance to outliers, the interquartile range is useful in identifying when a value is an outlier.
Formula to Calculate Interquartile Range.
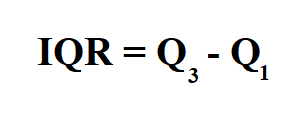
How to Calculate Q3 and Q1.
Q3 is the median of the upper quartile. Which is calculated by finding the median of the upper portion numbers.
Example:
Find the Q3 of the following data.
2, 3, 6, 7, 2, 5, 0, 2, 4
To find the median of the whole data set, we arrange the number in ascending or descending order, whichever you prefer.
0, 2, 2, 2, 3, 4, 5, 6, 7
Since this is an odd data set the median is clear and it is 3.
The numbers in the upper portion are those that are after 3, they are; 4, 5, 6, 7.
Since this is an even data set, we take the two middle numbers and divide by 2 to find the Q3.
= ( 5 + 6 ) ÷ 2
= 5.5
Therefore, 5.5 is the upper quartile (Q3).
Q1 is the median of the lower quartile. Which is calculated by finding the median of the lower portion numbers. For example.
Find the Q1 0f the following data.
2, 3, 6, 7, 2, 5, 0, 2, 4
Since we already know the median of this data, we will go straight to finding the Q1 from the arranged data set.
0, 2, 2, 2, 3, 4, 5, 6, 7
The lower portion of this data are all the numbers before 3 (median) and they are 0, 2, 2, 2.
Since we get an even data set, we take the two mid numbers add them and then divide by 2.
= (2 + 2) ÷ 2
= 2
Therefore, the Q1 is 2.
Example:
Suppose the median of the upper quartile is 50 and the median of the lower quartile is 25, calculate the interquartile range.
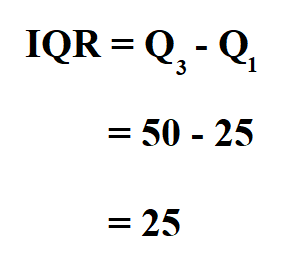
Therefore, the IQR is 25.