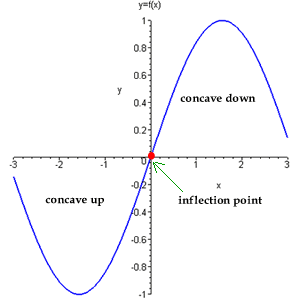
Prior to discussing how to calculate an inflection point, let us define what it is. An inflection point is a point on a curve at which a change in the direction of curvature occurs.
For instance, if your curve began as a concave up(CU) and later changed to concave down(CD), any point at which concavity changes from CU to CD or from CD to CU is the inflection point.
For instance if the curve looked like a hill, the inflection point will be where it will start to look like U.
Formula to Calculate Inflection Point.
We find the inflection by finding the second derivative of the curve’s function. The sign of the derivative tells us whether the curve is concave downward or concave upward.
Example:
Lets take a curve with the following function.
y = x³ − 6x² + 12x − 5
Lets begin by finding our first derivative.
y = x³ − 6x² + 12x − 5
y’ = 3x² – 12x
Then find our second derivative.
y’ = 3x² – 12x
y” = 6x -12
When we simplify our second derivative we get;
6x = 12
x = 2
This means that f(x) is concave downward up to x = 2 f(x) is concave upward from x = 2.
Therefore, our inflection point is at x = 2.