In this article, we will define and discuss how to calculate L.C.M. The least common multiple (L.C.M), also known as the smallest common multiple or the lowest common multiple can be defined as the smallest positive integer (0 not included) that is divisible by the numbers given.
This concept of L.C.M. is mostly used in the addition or subtraction of fractions.
How to Calculate L.C.M.
There are several formulas to get the L.C.M. of a list of number and they include:
Listing Multiples.
This is where you list multiples of each number until at least one of the multiples appear in all the lists. Find the lowest number in every list that’s the L.C.M.
Example 1:
Find the L.C.M. of 12, 16, 24.
Multiples of 12 = 12, 24, 36, 48, 60
And the Multiples of 16 = 16, 32, 48, 64, 80
Multiples of 24 = 24, 48, 72, 96
48 is the lowest number and common in all the lists so the L.C.M. OF 12, 16, 24 = 48.
Prime Factorization.
Here we find all the prime numbers of each number, list all the prime numbers with their highest power and multiply them to get the L.C.M.
Example 2:
Find the L.C.M. of 8, 9, 15
Prime factors of 8 = 2 x 2 x 2 also written as 2³
And the prime factors of 9 = 3 x 3 also written as 3²
While the prime factors of 15 = 3 x 5
The prime numbers with the highest power = 2³ x 3² x 5
L.C.M. of 8, 9, 15 = 2 x 2 x 2 x 3 x 3 x 5
= 360
Division Method.
This is where you write your numbers in a top row and starting with the lowest prime number that is divisible in at least one of your numbers, and bring down the result into the next row together with those that were not divisible. Continue doing this until your last row is left with 1’s. Get the product of the prime factors in the first column and that’s the L.C.M.
Example 3:
Find the L.C.M of the following numbers.
4, 9, 6
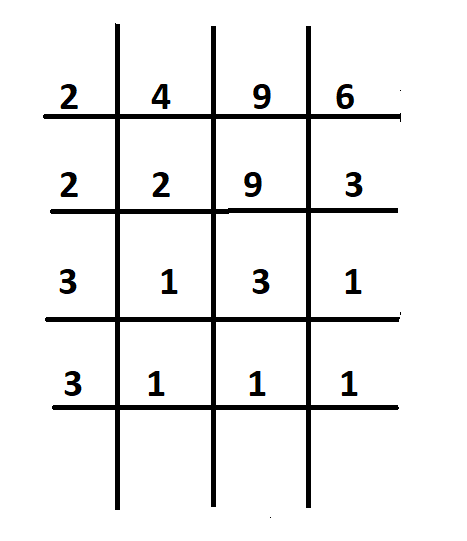
L.C.M. = 2 x 2 x 3 x 3
= 36